Discrete Mathematics 1.0.3

dla Samsung Galaxy Tab 3 V

Notatki, quiz, blog i filmy z dyskretnej matematyki na kursy inżynierskie. W większości tematów omawiane są diagramy, które ułatwiają naukę. Dotyczą prawie wszystkich ważnych tematów podanych poniżej

Rozdział 1 Teoria zbioru, relacja, funkcja, techniki dowodzenia twierdzeń

1. Ustaw teorię
2. zbiory policzalne i nieprzeliczalne
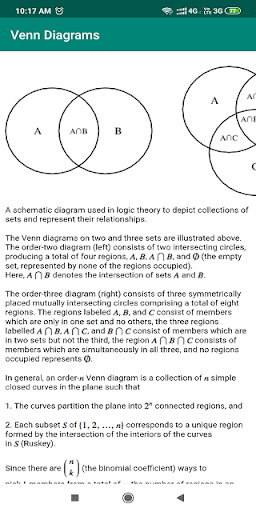
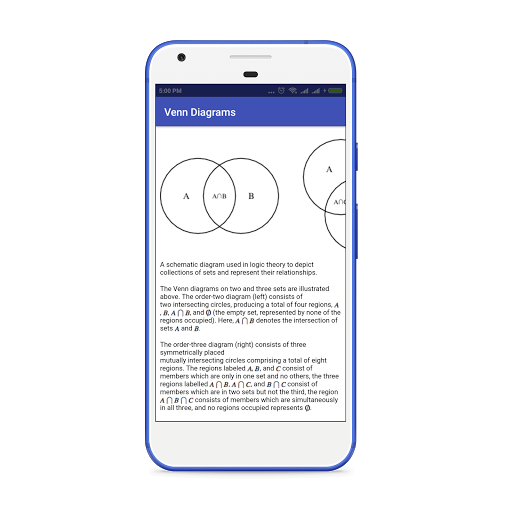
3. Diagramy Venna
4. dowody ogólnej tożsamości na zestawach Relacja w diagramach Venna
5. rodzaje relacji
6. skład stosunków
7. Relacja równoważności
8. Częściowa relacja porządkowa
9. Funkcja jeden do jednego
10. do i na funkcję
11. Funkcje odwrotne
12. Zasada dziobata

Rozdział 2 Struktury algebraiczne

1. Struktury algebraiczne
2. Grupa abelowa
3. Podgrupy
4. grupa cykliczna
5. Homomorfizm i izomorfizm grup
6. Pierścienie i pola

Rozdział 3 Logika zdań

1. Propozycja
2. Deklaracje warunkowe
3. Tabele prawdy twierdzeń złożonych
4. Logika i operacje bitowe
5. RÓWNOWAŻNOŚĆ EKSPOZYCJI
6. Równoważniki logiczne
7. Konstruowanie nowych równoważników logicznych
8. Predykaty
9. Kwantyfikatory
10. Nieskończone państwa i nieskończone przejścia między państwami
11. Maszyny skończonego stanu jako narzędzia rozpoznające język

Rozdział 4 Teoria wykresów

1. Wprowadzenie wykresów
2. Podstawowe warunki teorii grafów
3. Wykresy wyrówniarki
4. multigraf
5. Wykres izomorficzny
6. ścieżki, cykle, szlaki i obwody
7. Najkrótsze ścieżki
8. Ścieżki i obwody Euleriana i Hamiltona
9. Kolorystyka wykresu
10. numer chromatyczny
11. Homomorfizm i izomorfizm grup

Rozdział 5 Posesje, diagram Hasse'a i kraty

1. Posets, Hasse Diagram
2. zamówiony zestaw
3. Diagramy Hasse'a
4. Zestaw uporządkowany izomorficznie
5. dobrze uporządkowany zestaw
6. własności krat
7. ograniczone i uzupełnione sieci
8. Kombinatoryka
9. Permutacja i kombinacja
10. Twierdzenie dwumianowe
11. Wprowadzenie do zależności cyklicznych i rekursywnych
12. Relacje liniowe z stałymi współczynnikami
13. Rozwiązania homogeniczne